Modular hierarchical and power-law small-world networks bear structural optima for minimal first passage times and cover time
Abstract
Networks that are organized as a hierarchy of modules have been the subject of much research, mainly focusing on algorithms that can extract this community structure from data. The question of why modular hierarchical (MH) organizations are so ubiquitous in nature, however, has received less attention. One hypothesis is that MH topologies may provide an optimal structure for certain dynamical processes. We revisit a MH network model that interpolates, using a single parameter, between two known network topologies: from strong hierarchical modularity to an Erdős–Rényi random connectivity structure. We show that this model displays a similar small-world effect as the Kleinberg model, where the connection probability between nodes decays algebraically with distance. We find that there is an optimal structure, in both models, for which the pair-averaged first passage time (FPT) and mean cover time of a discrete-time random walk are minimal, and provide a heuristic explanation for this effect. Finally, we show that analytic predictions for the pair-averaged FPT based on an effective medium approximation fail to reproduce these minima, which implies that their presence is due to a network structure effect.
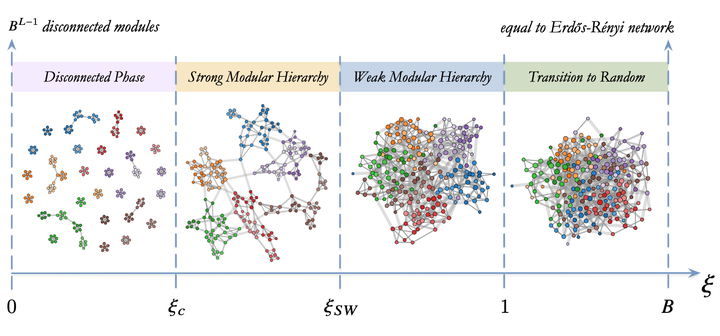 Topological phases of the SSMH model as a function of the structural control parameterξthat determines the degree of hierarchicalmodularity of the network
Topological phases of the SSMH model as a function of the structural control parameterξthat determines the degree of hierarchicalmodularity of the network